प्रस्तारे मित्र गायत्र्याः स्युः पादे व्यक्तयः कति |
एकादिगुरवश्चाशु कथ्यतां तत्पृथक् पृथक् ||
O friend, there are six letters in the fourth line of Gayatri meter. If we choose only 1 Guru, 2 G, 3 G, 4 G, 5 G, or 6 G, how many meters are possible?
This is a problem from Bhaskaracharya’s Lilavati.
How many meters with r Gurus (or Laghus) are possible in a prastaar for n syllables?
Pingala had developed a pratyay (method) to answer such questions.
Pingala’s sutra given in Chandahshastra for this method is:
परे पुर्णमिति | – (छन्दः शास्त्रम् 8.34)
This is a very cryptic code. It was only through Halayudha Bhatt’s commentaries on Chandahshastra in his work Mritasanjeevani (composed in 10th century CE) that people were able to understand this sutra. Halayudha has explained how to create a table of numbers which he called मेरु प्रस्तार.
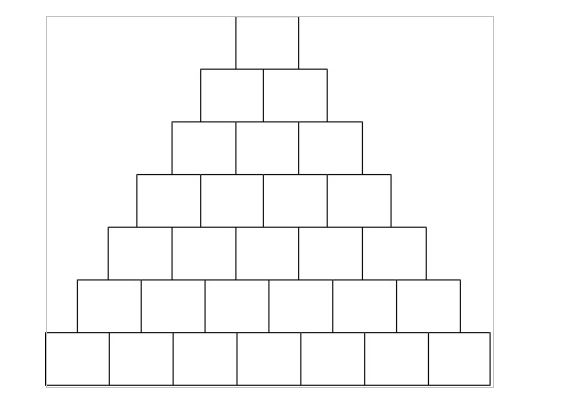
Table 1
Put one square in the first row. Refer to Table 1. Then put 2 squares below it in the second row. Below this put 3 squares in the third row. In the fourth row put 4 squares and so on. If you want the combinations for a meter having n syllables then create a table having n + 1 rows.
Write 1 in the square in the first row. Then put 1s in the squares at the ends of each row. Refer to Table 2.

Table 2
Numbers in the inner squares are got by adding the numbers in the two squares just above them. Refer to Table 3. Let me explain this by calculating the number for the middle square of the third row. Both the squares above this square contain 1, hence we get 1 + 1 = 2. The number in this square gives the number of meters having 1 Guru in a prastaar for 2 syllables.
Now let us calculate the value for the second square of the fourth row. The number in this square gives us the number of meters having 1 Guru in a prastaar for 3 syllables. The numbers in the two squares just above this square are 1 and 2.
Hence, we get 1 + 2 = 3.
Now let us calculate the value for the third square of the fourth row. The number in this square gives us the number of meters having 2 Guru in a prastaar for 3 syllables. The numbers in the two squares just above this square are 2 and 1. Hence, we get 2 + 1 = 3.
Now let us calculate the value for the second square of the fifth row. The number in this square gives us the number of meters having 1 Guru in a prastaar for 4 syllables. The numbers in the two squares just above this square are 1 and 3. Hence, we get 1 + 3 = 4.
The seventh row of this table gives us the answer to the problem posed at the beginning of this article. The first square of this row gives the number of meters when there are no Gurus. That is, all six syllables are Laghus. This can only be done in 1 way and that is, LLLLLL.
The second square of the seventh row gives us the number of meters when there is only when one G in a quarter. This can be done in 6 different ways, viz:
1) G L L L L L
2) L G L L L L
3) L L G L L L
4) L L L G L L
5) L L L L G L
6) L L L L L G
The third square of the seventh row gives us the number of meters when there are 2 Gurus in a quarter. And so on.
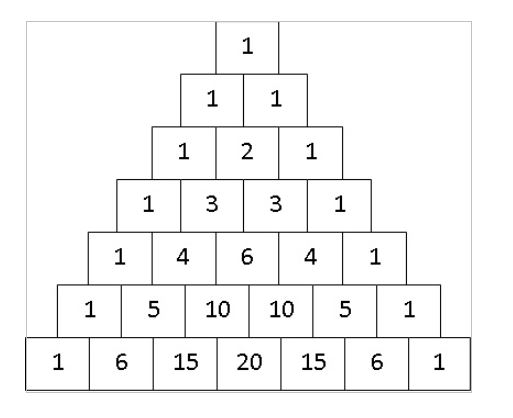
Table 3
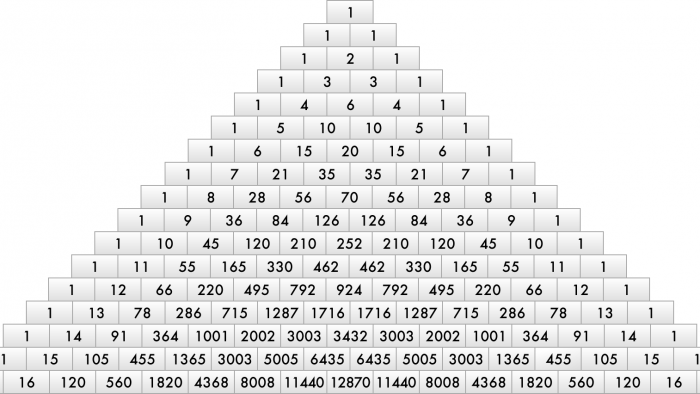
When we add up the numbers in all the squares of the seventh row it gives us the Sankhya for the prastaar of 6 syllables.
S6 = 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64
If we observe Table 3 closely, we can realize that the numbers in the squares are the binomial coefficients, nCr. Hence the number of metrical forms containing r Gurus (or Laghus) in a prastaar for n syllables is given by nCr.
Halayudha establishes that the basic rule for the construction of Meru Prastaar is the recurrence relation:
nCr = n-1Cr-1 + n-1Cr
Meru Prastaar’s form is like the steps to a hill. This must be the reason why Halayudha had called it Meru Prastaar. Meru is the name of a mountain.
Meru Prastaar is, what is popularly known as Pascal’s Triangle. But Pingala’s Meru Prastaar predates Pascal by at least 1800 years.
In the end, I would like to present Bhaskaracharya’s method for calculating the binomial coefficients:
एकाधेकोत्तरा अंका व्यस्ता भाज्याः क्रमस्थितैः |
परः पूर्वेण संगुण्यस्तत्परस्तेन तेन च ||
एकद्वित्र्यादिभेदाः स्युरिदं साधारणं स्मृतम् |
छन्दश्चित्त्युत्तरे छन्दस्युपयोगोऽस्य तव्दिदाम् ॥
मूषावहनभेदादौ खण्डमेरौ च शिल्पके ।
वैध्यके रसभेदिये तन्नोक्तं विस्तृतेभर्यात् ॥
The number of combinations of n things taken r at a time is
[n (n – 1) (n – 2) … (n – (r – 1))] / [1 x 2 x 3 x … x r]
This is useful in prosody to discover all possible meters, in architecture, medical sciences, Khandmeru, chemical compositions, etc.
Bhaskaracharya used to call Meru prastaar as Khandmeru.
Here I will conclude my series of six articles on mathematics from Pingala’s Chandahshastra.
Explore Pingala’s Algorithm Part I, II, III, IV, and V.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.