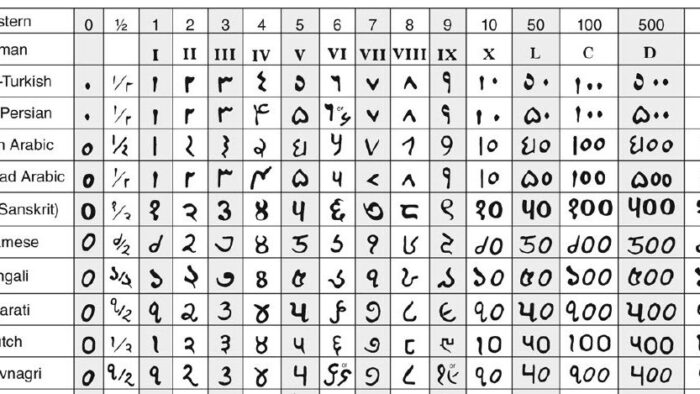
India represents the world in microcosm: here we have the simplest and most primitive number system in the world even as late as the twentieth-twenty-first century CE, as well as the most developed and elaborate number system in the world even as early as during the Vedic period.
This article was intended to be purely informative, and to serve no purpose other than pointing out three uniquely special features of Indian numbers and numerals. But, inevitably, I found one more strong piece of evidence to confirm the OIT (Out-of-India Theory of Indo-European Origins) which is so irrefutably established by the textual, linguistic and archaeological evidence.
Numbers and numerals form an important, even a vital, part of life. This point is too elementary to waste time here in elaborating why it is so. The fact is that India occupies a unique place in the whole world in the field of numbers and numerals, and the purpose of this article is to place these unique features on record:
1. The Concept of Numbers.
2. The Written Numeral System.
3. Indo-Aryan Numbers.
1. THE CONCEPT OF NUMBERS
The very idea of numbers is something which seems very natural to us. But is it really so? Incredible though it may appear to us, there are some very primitive or simple languages in the world which do not even have concepts or names for numbers up to ten (the number of fingers on a human pair of hands, which would seem to be the natural base for counting). This is mainly so among the Australian aboriginal languages. The following examples of some Australian aboriginal language numbers will make this clear:
Nunggubugu:
1. Anyabugij
2. Wulawa
3. Wulanybaj
4. Wulal wulal
There are no number words beyond four.
Kamilaroi:
1.Mal
2.Bular
3.Guliba
4.Bular bular
5.Bular guliba
6.Guliba guliba
There are a specific number of words for numbers up to three, and the same words are combined to produce numbers from four to six, at least.
Gumulga:
1.Urapon
2.Ukasar
3.Ukasar urapon
4.Ukasar ukasar
5.Ukasar ukasar urapon
6.Ukasar ukasar ukasar
This language has a specific number of words for one and two, and these are combined to produce numbers from three to six.
A related language Mabuiag has similar words from one to six:
1.Urapun
2.Okosa
3.Okosa urapun
4.Okosa okosa
5.Okosa okosa urapun
6.Okosa okosa okosa
And then there is a number word for seven and any other number after 7:
7 or 7+. ras.
There are apparently a few rare languages in the extremely isolated portions of areas within Papua-New Guinea, interior Africa and Patagonia (the southern half of South America) which have similar structures in which the numbers do not go beyond six or ten and are based on words from one to three.
But India represents the world in microcosm: here we have the simplest and most primitive number system in the world even as late as the twentieth-twenty-first century CE, as well as the most developed and elaborate number system in the world even as early as during the Vedic period (extending back beyond 3000 BCE, or, even as per the now-discredited AIT version of Vedic history, to 1200 BCE).
The simplest and most primitive number system in the world (the word “primitive”, it must be emphasized here, is not a deprecatory word) is found in the Andaman Islands in India. Formerly (as per older colonial records, and I have myself quoted them in an earlier article) it was believed in fact that the Andamanese languages had numbers only for one and two. However, it appears this is not so.
The following are the number words in the Aka-bea-da (Greater Andamanese) language, which only has words from one to five:
1: Obatul
2: Ikpaurda
3: Edarobai
4: Eijipagi
5: Arduru
But an even simpler and more primitive form of number system, the simplest and most primitive form in the world, is found in the Onge language, which has numbers only from one to three, and any number above that is represented by a word ilake which does not mean “four” but specifically means “many”:
1: Yuwaiya
2: Inaga
3: Irejidda
On the other hand, as early as the Vedic Samhitas, we had words in India for very high numbers. The Yajurveda, for example, in the course of a hymn (Yaj. 17.2), casually lists the following words for numbers from ten (101 or 10) to one trillion (1012 or 1, 000, 000, 000, 000):
101: daśa
102: śata
103: sahasra
104: ayuta
105: niyuta
106: prayuta
107: arbuda
108: nyarbuda
109: samudra
1010: madhya
1011: anta
1012: parārdha
It is obvious that while, for ritual purposes, the enumeration in this hymn stops at 1012, logically there is clearly an understanding of the infinite nature of this mathematical series and of the idea that these are just the first steps in an infinite series of numbers each being a multiple of the previous number by ten. This becomes apparent from countless references and number words in the ancient Vedic and Sanskrit texts, but most particularly in certain texts which play with mathematical ideas. For example, the Lalitavistara, a Buddhist text, actually describes an even more elaborate system (where some of the above words from the Yajurveda are now replaced by other words, and all the names are given in multiples of hundred. Here in fact some of the above words, like ayuta and niyuta, are given higher values):
103: sahasra
105: lakṣa
107: koṭi
109: ayuta
1011: niyuta
1013: kaṅkara
1015: vivara
1017: akṣobhya
1019: vivāha
1021: utsāṅga
1023: bahula
1025: nāgabala
1027: tiṭilambha
1029: vyavasthānaprajñāpti
1031: hetuhila
1033: karaphū
1035: hetvindriya
1037: samāptalambha
1039: gaṇanāgati
1041: niravadya
1043: mudrābala
1045: sarvabala
1047: visaṁjñāgati
1049: sarvasaṁjña
1051: vibhūtaṅgamā
1053. tallakṣaṇa
The text does not stop there: it points out that this is just the first of a series of nine counting systems that can be expanded geometrically, and then goes on to mention the names of the culmination points of each of the nine systems (starting with the number 1053 above, as tallakṣaṇa, dhvajāgravatī, dhvajāgraniśāmaṇī, vāhanaprajñapti, iṅgā, kuruṭu, kuruṭāvi, sarvanikṣepa, and agrasārā), culminating in a large number, 10421, or one followed by 421 zeroes! This text, and many other Sanskrit texts, go even further in indulging in flights of fantasy involving even higher numbers. The point is not whether such incredibly high numbers could possibly serve any practical purpose: obviously they could not! The point is that the ancient Indian theoretical concept of numbers had a vision that was limitless.
India, therefore, occupies a unique position in the world: on the one hand, it has even in the twenty-first century the Onge language with no number words of its own beyond three (i.e. the simplest number system in the world), and on the other, it had even in ancient times:
a) number words for numbers as high as 1053, and, in theory, even as high as 10421, and in further theory, going into unimaginably and fantastically high numbers beyond even that;
b) the concepts of zero, finite numbers and infinity (and, in Jain texts, even different categories of what are now called transfinite numbers);
c) the concept of fractions (found even in the Rigveda, in the Puruṣa sūkta, Rig. X.90.3, 4);
d) the concept of negative numbers.
All this is apart from the highly developed state of almost every branch of mathematics in ancient India.
To be continued…
This article was first published on IndicFacts.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.