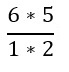लौकिके वैदिके वापि तथा सामायिकेऽपि य: ।
व्यापारस्तत्र सर्वत्र सङ्ख्यानमुपयुज्यते ॥
कामतन्त्रेऽर्थशस्त्रे च गान्धर्वे नाटकेऽपि वा।
सूपशास्त्रे तथा वैद्ये वास्तुविद्यादिवस्तुषु ॥
छन्दोऽलङ्कारकाव्येषु तर्कव्याकरणादिषु ।
कलागुणेषु सर्वेषु प्रस्तुतं गणितं परम् ॥
सूर्यादिग्रहचारेषु ग्रहणे ग्रहसंयुतौ ।
त्रिप्रश्ने चन्द्रवृतौ च सर्वत्राङ्गीकृतं हि तत् ॥
(In worldly life, in Vedic learning, in religious practice, in business, in everything, Mathematics is useful. In romance, economics, in music, dance and drama, in cooking, medicine and in architecture, in prosody, poetry, logic and grammar, and in all the arts, Mathematics reigns supreme. It is used in calculating movements of the Sun and other heavenly bodies.)
बहुभिर्विप्रलापै: किं त्रिलोक्ये सचराचरे ।
यत्किञ्चिद्वस्तु तत्सर्वं गणितेन विना न हि ॥
(Whatever there is in all the three worlds, which are possessed by moving and non-moving beings- all that indeed cannot exist as apart from Mathematics.)
The above verses are from the book Ganitasarasangraha written around 850 CE by a Digambara Jain monk Mahavira (815 – 877 CE).
You might be wondering what has art got to do with Mathematics? And of all the things what has mathematics got to do with cooking? As an answer to this, lo behold, here is a problem from Bhaskaracharya’s (Bhaskaracharya II) (Born 1114 CE) book Lilavati :
एकद्वित्र्यादियुक्त्या मधुरकटुकषायाम्लकक्षारतिक्तैः।
एकस्मिन् षड्रसैः स्युर्गणक कति वद व्यंजने व्यक्तिभेदाः।।
(In how many different ways can we garnish a dish using six different types of flavouring substances – sweet, bitter, salty, sour, pungent and hot, taking them by ones, twos, threes, and so on at a time?)
Bhaskaracharya had composed Lilavati in 1150 CE to teach Mathematics to his daughter Lilavati, after whom he had named the book. This book which is written entirely in verse form, covers arithmetic, algebra, geometry, mensuration, combinatorics, number theory, and other basic topics. This book was used as a standard textbook for almost 700 years.
Coming back to the above seemingly culinary problem, let us try to solve it using mathematics –
I may not garnish my dish at all. Now, this can only be done in one way. Remember this subtotal, 1.
I can garnish the dish using all the six ingredients. Now, this can be done in only one way. Remember this subtotal, 1.
I may garnish the dish using any one of the six flavouring substances. This can be done in six different ways. Subtotal = 6.
I may garnish the dish using any five of the six ingredients. This can be achieved by leaving out anyone of the six ingredients. Now, this can be done in six different ways. Subtotal = 6.
Now, I want to garnish the dish using any two of the six flavouring substances. In how many different ways can this be done?
In the same chapter of Lilavati from which the given problem is taken, Bhaskaracharya has given us the formula for calculating the number of combinations of ‘n‘ things taken ‘r‘ at a time as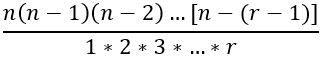
Using modern notation the same formula is given as ![]()
Using this formula let’s calculate in how many different ways I can garnish my dish using any two of the six different flavouring substances-
= 15. Hence, this can be done in 15 different ways. Subtotal = 15.
I may garnish my dish using any three of the six ingredients. This can be done in 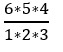 = 20 different ways. Hence, subtotal = 20.
= 20 different ways. Hence, subtotal = 20.
I may garnish my dish using any four of the six ingredients. This can be done in 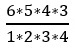 = 15 different ways. Hence, subtotal = 15.
= 15 different ways. Hence, subtotal = 15.
Hence, I can garnish my dish in 1+6+15+20+15+6+1=64 different ways.
This was the kind of awareness amongst ancient and medieval Indians about mathematics and its applications in daily life. Ancient Indians considered Mathematics as the most significant subject. This is evident from this verse from Vedanga Jyotisa (500 BCE).
यथा शिखा मयूराणां , नागानां मणयो यथा ।
तद् वेदांगशास्त्राणां , गणितं मूर्ध्नि वर्तते ॥
Like the crest of a peacock, like the gem on the head of a snake, so is mathematics at the head of all knowledge.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.