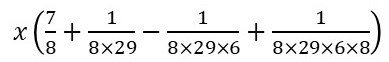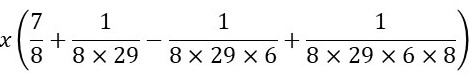Over the last two to three decades, a particular concept, related to math, is gaining quite a popularity amongst the common Indians. It’s called Vedic Maths. This comprises of certain formulae (written in Sanskrit), which may be used as short cuts to ease an otherwise tedious calculation. The author would like to keep his fingers crossed about the usability and applicability of these “short cuts”, but does all this have anything to do with veda-s, the way it is proclaimed as “Vedic Math”? It was Shri. Bharathi Krishna Tirthaji, who wrote these formulae somewhere in between A.D. 1911 and 1918. Clearly these are not much older than 100 years. And the veda-s? How old are they?
Indians can enjoy this yet another feather in their cap, that veda-s are now regarded (almost, all over the world) as the first ever literature in the history of mankind, with ऋग्वेद (Rugveda), being the oldest amongst all the veda-s. In which year these were first constructed or “seen” or “conceived” or “realized”?
While Western scholars have estimated that Rugved might not have been constructed before 3 to 4 thousand years B.C., some of the Indian scholars feel that it must have been much older than this. A Sanskrit scholar Dr. P. V. Vartak had proposed and almost shown that Rugved was created more than 20000 years back. While many Indians, essentially disciples of Western scholars, like to attribute this estimate of Vartak as an offspring of his bigotry, they would never feel that the Western estimates of Rugved might well have been out of their jealousy towards the rich and blossomed oriental culture!
We will not go into this conflict. Instead we will talk about the mathematical aspects, related to veda-s, vedanga-s and so on. Our mythological stories are filled with यज्ञ (yadnya, meaning sacrifice) and the related auspicious deeds to such an extent that the word veda automatically portrays the pictures of yadnya, the altar, the fire, the ghee that is getting poured, the sages, ascetics etc. Whether all those so called rituals are or were of any practical worth is a separate topic for research, but one thing may be noted that in most of these, typical structures, carefully constructed, used to be present. Here ‘careful’ refers to “mathematically precise”! And through this, we realize the amount of mathematical knowledge that our ancestors had, may be 5000, if not 20000, years back. Of course, it’s quite saddening that now only one particular treatise, known as शुल्बसूत्र (Shulbsootra) is available. But even this is sufficient for our purpose, for the time being. Of course, somebody can raise objection by saying that eight different Shulbsootra-s (बौधायन, आपस्तंब, सत्याषाढ, वाधुल, मानव, मैत्रायणी, वराह, कात्यायन) are available, at present. It’s true, but the author wants to convey that no other text on maths in the era of veda-s is available. The word शुल्ब (shulb) stands for thread and सूत्र (sootra) means formula. The treatise contains many readymade formulae for some constructions. The measurements were carried out using a thread, and hence the name!
As per a tradition, there used to be three places for the fire in the house of Agnihotri-s. For this, there used to be three different geometrical figures drawn on the floor of their houses. One of these used to be circular, another one semi-circular and the third figure used to be a square. It was mandatory that the area of these figures should be equal and so people needed to know the required proportion between the radius of circle and side of the square. (It may be noted that it’s not possible to have a square whose area exactly equals the area of a circle, but one can have an approximate one!) Also, for certain purposes (regarding directions), people needed to know the proportion of the lengths of a right angled triangle. In the verses regarding this, we clearly see that they knew Pythagoras theorem, much before Pythagoras was born! And, of course, there are many more results from geometry. Let us see, how far we can go!
The geometric part of the Baudhayan Shulbsootra-s starts with the methods of drawing a square. Two different methods are given there, one using various circles and the other using triangles. It should be noted that for drawing a square, only a straight-edge is not sufficient. Reader can try this at home. So writing a method or two is certainly not a waste of space. But the more interesting facts are a bit ahead…
समचतुरस्रस्याक्ष्णयारज्जुर्द्विस्तावर्ती भमिं करोति |
(samachaturasrasyaakshnayaarajjurdvistaavarti bhamim karoti|)
This means that the area of a square, with side equal to that of अक्ष्णयारज्जू (akshanayaarajjoo) of an original square, is double the area of the original square. The word अक्ष्णयारज्जू (akshanayaarajjoo) refers to the diagonal of a square. The reader must be knowing the fact that in a square, the diagonal is “root two” times its side. Clearly, the area of a square, whose side is the diagonal of an original square, would be twice the area of the original square. How did they prove that the diagonal is “root two” times the side? Well, they must have used Pythagoras’ theorem… but wait! Pythagoras was born much later! So, the author of Baudhayana Shulbsootra-s knew the interesting result of a right angled triangle, much before Pythagoras!
If you are not convinced with this argument, let us see what next we find…
त्रिकचतुष्कयोः द्वादशिकपञ्चिकयोः पञ्चदशिकाष्टिकयोः सप्तिकचतुर्विंशकयोः द्वादशिकपञ्चत्रिंशिकयोः पञ्चदशिकषट्-त्रिंशिकयोरित्येतासु उपलब्धि:।
(trikachatushkayo: dvaadashikapanchikayo: panchadashikaashtikayo: saptikachaturvinshakayo: dvaadashikapanchatrinshikayo: panchadashikashattrinshikayorityetaasu upalabdhi:|)
Here the author is talking about rectangular shape, the rectangles having specific side lengths. What are these? त्रिकचतुष्कयोः means 3 and 4, द्वादशिकपञ्चिकयोः means 5 and 12, पञ्चदशिकाष्टिकयोः means 8 and 15, similarly, 7 and 24, 12 and 35 and finally 15 and 36 respectively. But why these particular sides only? If you observe these numbers carefully, you will see that these numbers are the smaller numbers in the standard Pythagorean triplets! If a rectangle (or a right angled triangle) has its sides 3 and 4, then its diagonal (or hypotenuse, in case of a right angled triangle) is of length 5. Recall these triples: (5, 12, 13), (8, 15, 17), (7, 24, 25), (12, 35, 37), (15, 36, 39). Do you see that the smaller numbers in each of these brackets are mentioned in the above verse? Is it just a coincidence? Is it really the case that the authors of the shulbsootra-s just stumbled upon these numbers, merely by an accident?
In the Katyayan Shulbsootra, we find something interesting about a term, called विशेष (vishesh). It says,
करणिं तृतीयेन वर्धयेत्तच्च स्वचर्तुथेनात्मचतुस्त्रिंशोनेन स विशेष इति विशेषः|
(karanim truteeyen vardhayettachcha svachaturthenaatmachatustrimshonen sa vishesh iti vishesh:|)
Here it is given the definition of विशेष (vishesh). Consider a side of a square. Increase its length by its one third. Then further increase it by one fourth of its one third and then reduce it by one thirty-fourth of the one fourth of the one third. This new length is known as विशेष (vishesh). It was known that a square formed with side equal to विशेष (vishesh) has twice the area of the original square.
Let us try to write this mathematically. Suppose the side of the original square was x. Add one third of x to it. So, we have, x + x /3 . Now add one fourth of the one third. Thus, the new length equals 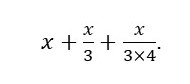
Now subtract one thirty-fourth of the last term. This should give us vishesh. Hence, vishesh equals . ![]()
This doesn’t appear elucidating at all, right? Now if we put x = 1 (The reader can actually do this, using calculator), the length of vishesh would be ,
which is approximately 1.4142156. If this also doesn’t strike anything, then just square it and you will realize that this 1.4142156 is very close to square root of 2. In fact, this value is quite acceptable even in modern times also, since, by calculator the value of square root of 2 up to 7 digits is 1.4142136, slightly different from the value obtained above. And now no need to repeat that if 1 is the side of the original square, then the square with side equal to root 2, would have twice the area of the original square. So draw a square of any length, get the vishesh of its side and with vishesh as the side, draw another square. This new square has double the area of the original square.
One question strikes at this point. If they already knew that diagonal of a square is “root two” times its side, why to take this lengthy path? It seems that through this, they were trying to get approximate value of square root of two. They might very well be knowing that this is only approximate, and not the exact, value of root two. This is not an attempt to safeguard our ancestors, for we have already seen the words like सूक्ष्म and स्थूल, used in similar context.
The use of a ‘kind of’ series for obtaining the value of root two is no wonder! While depicting the method of obtaining a square whose area equals that of a circle, we find that the side of the square should be ,
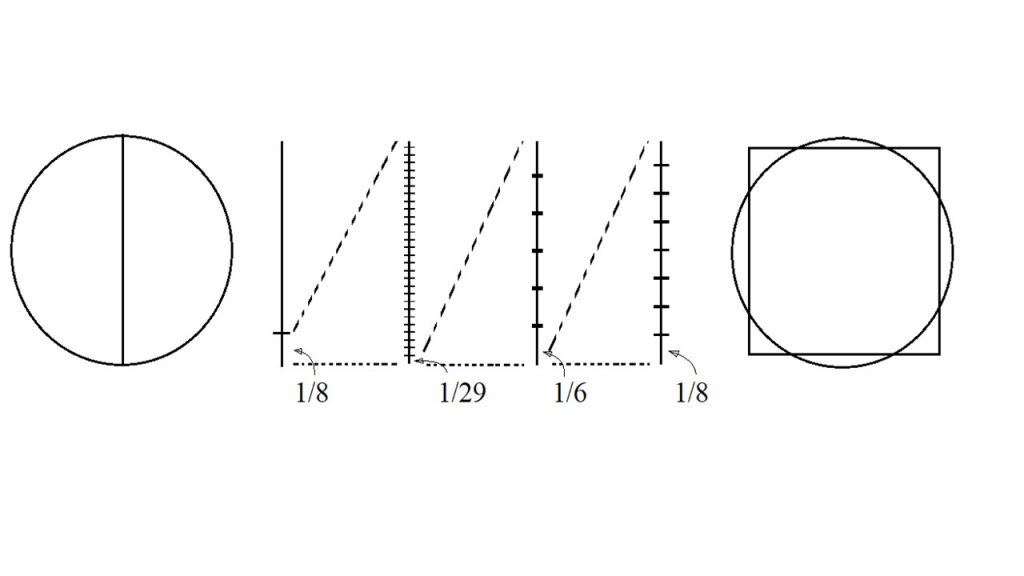
where x is the diameter of the circle. This helps in getting a square whose area approximately equals the area of the given circle. To understand a bot more about this ‘kind of’ series observe the following figure.
Start with the circle on the left side. Its diameter is shown separately to its right. Make its 8 equal parts. Keep its 7/8th part aside. The remaining 1/8th part is expanded and shown to its right. Make its 29 equal parts. Consider its 1/29th part, expanded and shown to its right. Make 6 equal parts of this part. Finally this 1/6th part is expanded and shown to its right. Make its 8 equal parts. Again observe that side of the square should be .
Make 8 equal parts of the diameter. Keep 7/8th part of the same aside. To this, add 1/29th part of the remaining 1/8th part. But after that, subtract 1/6th part of the added 1/29th part. Finally add 1/8th part of the subtracted 1/6th part. Draw a square with whatever length you get, as shown in the rightmost. The area of this square will be approximately equal to the area of the original circle. How good is this observation? If we let diameter of the circle to be 1, then its area comes out to be 0.7853981634, while this method gives area of the obtained square as 0.7769910526! Yes, it’s a good approximation!!
The exact date of the veda-s is a debatable issue, but now it is accepted that the veda-literature is the oldest. This suggests that the treatise like Shulbsootra too are much older than the so called revolutionary work of the Greek mathematicians. The problem with Indians is that, due to certain political reasons, we were taught (or cultured) to hate or belittle or ignore our own ancestors and their monumental work. While we don’t hesitate in praising the Western culture, we just shiver to accept that ours too was a blossomed one! While the scientific and mathematical progress in the Western part in the last three hundred years is undoubtedly praiseworthy, a word of appreciation towards Indians is looked upon as self-deceit. The stories suggesting the existence of aeroplanes, test-tube-babies and super computers might not be true; these might well be just myths! Nevertheless, what we had was commendable!
A great Marathi poet Kusumaagraj has written a poem समिधाच सख्या या (samidhaach sakhyaa ya) about his own poetry, where he himself says that his poetry is quite prosaic (and not poetic). What was he trying to achieve then? He replies, तव आंतर-अग्नी क्षणभर तरि फुलवावा (tav aantara-agni kshanabhara tari phulavaavaa). This means that his poetry was written to instigate the inner feelings of the readers, at least for a moment or two! As we come to the end of this article and the series itself, I feel the same as expressed by Kusumaagraj. The purpose of this series was तव आंतर-अग्नी क्षणभर तरि फुलवावा. Whether was I successful or not, is left to the readers.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.