(Ancient Indian Mathematical Treasure is a new series of articles by Salil Sawarkar, introducing the rich mathematical heritage of our country. This is the third article in the series. Read the first three articles here, here and here.
From nothingness (शून्य) to as big as 1017 (परार्ध) or 1023 (महाक्षोभ)! In fact, some claim that we had coined terms for the numbers even larger than 1023. But why did Indians think of such large numbers?
Do we need such large numbers in our day to day conversation? Have you heard of anyone having such a huge salary? Or, for that matter, anyone’s age being as large as that? Or could it be possible that the kings of bygone era were donating wealth in such proportions to scholars? If not, then what is the point of having such large numbers?
It is true that in our day to day life, we may not need such enormous numbers. But who says that the sole purpose of math is to satisfy our day to day needs? Should basic arithmetic be the only purpose of mathematics? You might argue here by pointing out that such a line of arguments doesn’t answer our question! “Why such big numbers?”
It is estimated that there are billions and billions of stars in our milky way, and there are billions and billions of galaxies in the universe. The distances between stars are enormous… moreover the distances between them are increasing day by day. The entire universe is expanding. The energy emitted by stars in the form of heat or light is massive. The gravitational force that is being exerted by these massive spheres in the space is ridiculously high. And what about the age of the universe? All this calls for extremely large units.
The S.I. unit of distance is meter. This is a standardized unit for measuring lengths or distances. Nevertheless, in the field of astronomy, people prefer other units, like the Astronomical unit, light year, par-sec etc. Astronomers find it convenient to express the enormously large distances using these new units.
Aryabhata, one of the greatest geniuses of all times, too was concerned with a lot of difficulties that he was facing in his study of astronomy. The decimal system was fully developed and so expressing a large quantity like “twelve thousand three hundred and forty five” was as easy as writing 1, 2, 3, 4, 5. But even this system wasn’t sufficient for his work. Another nagging problem was this that he had to create verses for writing his treatise. The verses should have been small in size, so as to make them easy to remember, and yet capable of expressing a lot! The only solution that he could see was to create another way of expressing numbers, that is, to create another number system. In this system, different words could be created to mean different numbers. These new words could be fitted into verses. Moreover, to express large numbers, he required very small words. Recall that in the last article, we talked about the values of trigonometric functions at different angles. While writing a verse about the values of trigonometric functions, Aryabhata uses the words like मखि, भखि, फखि to mean 225, 224, 222, respectively. Otherwise, for expressing these numbers he would have needed words like पञ्चविंशत्यधिकं द्विशतम्, चतुर्विंशत्यधिकं द्विशतम् and द्वाविंशत्यधिकं द्विशतम्.
Aryabhata’s work in math can be compared to Panini’s work on Sanskrit grammar. In order to have small words capable of expressing a lot, Panini created (kind of) new words, which he called Pratyahara. Without a clear understanding of these Pratyahara-s, one cannot understand Panini’s work. The same is true for to Aryabhata. In his treatise, Aryabhatiya, after the initial salutations, which was a common feature in those days, Aryabhata writes…
वर्गाक्षराणि वर्गेऽवर्गेऽवर्गाक्षराणि कात् ङ्मौ य:।
खद्विनवके स्वरा नव वर्गेऽवर्गे नवान्त्यवर्गे वा॥
(vargaaksharaani varge avarge avargaaksharaani kaat nmau ya:|
khadvinavake svaraa nava varge avarge navaantyavarge vaa||)
These lines seem cryptic at first sight, especially for those with only as elementary knowledge of sanskrit and mathematics.
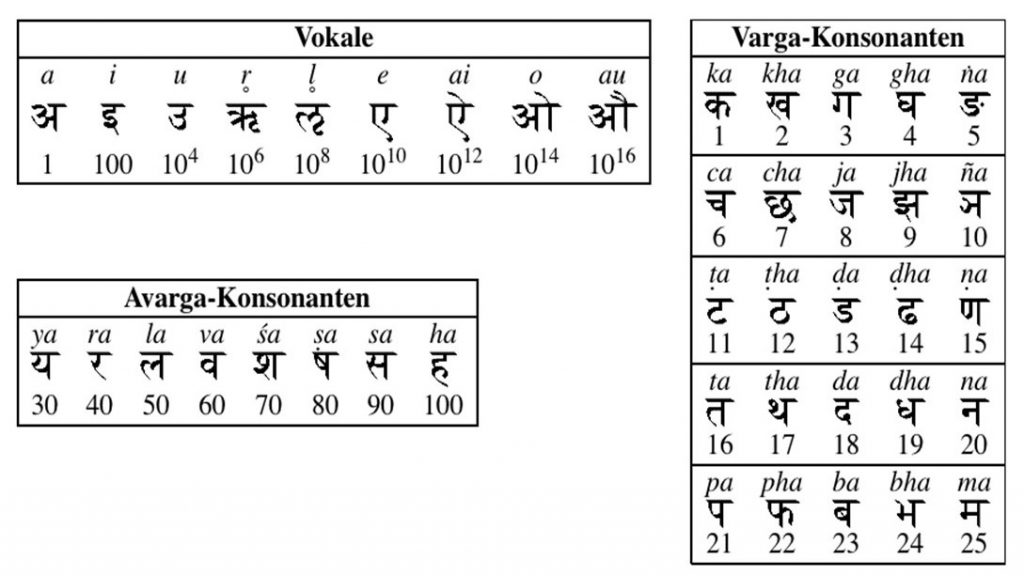
Actually, this is the most important verse of Aryabhata, for it’s here that he explains his new code. If this is not understood, the whole treatise remains a collection of meaningless sequences of jumbled letters. According to him, the letters from क् to म्, are assigned values of 1, 2,…, 25, respectively. Then the letters य् onwards up to ह् are assigned values be 30, 40,…, 100, respectively. For each of the 9 vowels (अ, इ, उ, ऋ, लृ, ए, ऐ, ओ, औ), he assigns two different values, 1 or 10, up to, 1016 (मध्य) or 1017 (परार्ध), according to whether these are placed at the वर्गस्थान or अवर्गस्थान.
The author is well aware that the above paragraph is nowhere adequate for a reader to get to know Aryabhata’s terminology completely. Explaining everything is beyond the scope of this article. Still, just to encourage the readers to delve into Aryabhata’s work, consider मखि. Start from right, ख् + इ. The letter ख् gets the value 2 and the vowel इ gets the value 100. Thus, खि stands for 2 × 100 = 200. Now comes म, which gets the value 25. Add 200 to 25, and you get 225! The same applies to other terms. खि stands for 200 and भ stands for 24. So भखि would mean 224. Similarly, फखि means 222, as फ means 22. It’s a very small attempt of the author to make reader aware of such and such terms, used by Aryabhata and to throw some light on the need of such cryptic terms.
According to Aryabhata (and he is absolutely right) obtaining the square (वर्ग) of a quantity and the area of a geometric square are similar operations. The same applies to calculating the cube of a quantity and getting volume of a solid cube (घन).
वर्ग: समचतुरस्र: फलं च सदृशद्वयस्य संवर्ग:।
सदृशत्रयसंवर्गो घनस्तथा द्वादशाश्रि: स्यात्॥
(varga: samachaturasra: phalam cha sadrushadvayasya samvarga:|
Sadrushatrayasamvargo ghanastathaa dvaadashaashri: syaat||)
Of course, finding squares and cubes is a bit straight forward job; but the reverse is not so easy. But here too, Aryabhata did a great job by proposing a new method of finding square roots and cube roots of numbers. This is today called the “long hand rule” and is taught to children in middle-school.
Despite his numerous contributions to mathematics (some of which will be discussed in some later articles), Aryabhata is more famous for his work on astronomy. As a tribute to his work in this field, the first satellite launched by India was named after him. It was named Aryabhatta, which is what his name was mistakenly believed to be. However, he himself has mentioned his name as Aryabhata in his treatise.
He also attempted to find the diameters of various heavenly objects, including those of the Earth, Sun, Moon and the then known planets of the solar system. He writes,
नृषि योजनं ञिला भूव्यासोऽर्केन्द्वोर्घिञा गिण…
(nrushi yojanam nilaa bhoovyaasoऽrkendvorghinaa gina…)
Deciphering this verse will require some efforts; and this is not the complete one. Only the beginning of the verse is written here. According to Aryabhata, one yojana (योजन) is as long as (the total height of) 8000 (षि) men, that is, (assuming height of a man as 5 feet) approximately 40000 feet. With this understanding in mind, let us see what the verse is saying. The diameter of the Earth (भू) is 1050 yojanaas (ञिला), and the diameters of Sun and Moon (अर्केन्द्वो:) are 4410 yojanaas (घिञा) and 315 yojanaas (गिण), respectively. Note that 40000 feet is approximately 12 km. Thus, the diameters of these huge spheres, according to Aryabhata, turn out to be 12600 km, 52920 km and 3780 km respectively. The diameter of the Earth obtained by modern science is 12800 km! Surprised? Well, I was wonder-struck! The diameter of Moon is now calculated to be 3500 km, which too is very close to the figure (3780), given by Aryabhata.
The only person who never commits a mistake is the one who never tries! Even veterans fumble and the champions stumble! Remember that it’s not always your “right answers” that count. At times, even your mistakes too! And so, there is nothing wrong in discussing the failures of our ancestors as we may still learn a lot through their mistakes. Thinking only about the glorious past might make us self-conceited.
The diameters obtained by Aryabhata for the Sun and other planets like Mercury, Venus, Mars, Jupiter and Saturn are far away from the actual ones, obtained by modern science. The reasons for some of his assumptions in carrying out all these calculations are still not fully known. We need to dig deep to understand his method completely. Such attempts may open new vistas of knowledge and let more light in.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.