(Ancient Indian Mathematical Treasure is a new series of articles by Salil Sawarkar, introducing the rich mathematical heritage of our country. This is the third article in the series. Read the first two articles here.and here.
Understanding abstract objects like numbers is the beginning of all mathematics. In this piece we are interested in getting a glimpse of what inspired our ancestors to undertake the mathematical journey and how far they went ahead. However, we need not stick ourselves to pure mathematics. Other subjects too can contribute in understanding our ancestors’ thinking better. Let us see what language has to offer at this point. As we learn Sanskrit and other languages, one basic difference becomes clearly visible. While in most of the other languages, there are only singular and plural cases, in Sanskrit we also see the presence of the dual. Why do we have separate forms of words to describe things which are “two” in number, is a good question to ask. However what people don’t ask (or care to ask) is that, if द्विवचन is/was required, then why not have त्रिवचन, चतुर्वचन and so on? Why not have separate word forms for “three” quantities, “four” quantities and so on?
In the last article, we saw that for describing “two”, our ancestors freely used the words for the factors of human body, like, कर, बाहु, नयन, कर्ण etc. This terminology suggests a lot! It’s a known fact that Indians were (and may be, are) quite ahead in the field of spirituality. The spiritual practices strongly demand introspection. And the introspection usually starts with our body. Recall what Kalidas had said: शरीरमाद्यं खलु धर्मसाधनम् ।
Let us observe ourselves, carefully: I am one. I have one body, one soul, one mind, one heart, one intellect! Similarly, I have two hands, two legs, two eyes, two ears! But I am still left with so many other factors. What about teeth, hair, bones, veins, muscles, cells? Is it so that here lies the reason for the absence of त्रिवचन, चतुर्वचन in the language? Note that I am carrying various “single” factors and various factors in pairs, but after that do I have many triplets or quadruplets of factors? After considering hands, feet, eyes etc., I realize that whatever I am left with, it is in abundance! I have 32 teeth, more than 200 bones, hundreds of muscles and millions of hair. The realization of this “multitude” made the language stop the inclusion of more “numbers” in it. But, at the same time, mathematics continued the inclusion of more words in it. Bhaskaracharya gives a list of words for the numbers from 1 (एक), 10 (दश), 100 (शत), 1000 (सहस्र) up to as large as 1017 (परार्ध) and says that, “सञ्ज्ञा: सङ्ख्याया: स्थानानां व्यवहारार्थं कृता पूर्वै:”, i.e., these numbers are created long back for day-to-day practices. In the ninth century, Mahaviracharya’s ‘Ganita-Saara-Sangraha’ mentions terms from 1 (एक) to 1023 (महाक्षोभ). It’s interesting to note that the Roman Numeral System had L, C, D, M for 50, 100, 500, 1000 respectively and stops! With the symbols I, V, X, L, C, D, M, the largest number which one can write doesn’t exceed even 5000!
Let us not forget that math is not just a game of numbers. It starts with numbers but works on shapes too! (Note that the word “figure” stands for numbers as well as for shapes). Indians have shown keen interest in the calculations of areas and volumes of different shapes. An important aspect of geometry is that of similarity, which leads to trigonometry, which in turn finds applications in getting the heights of mountain peaks and depths of seas and oceans. The reader is sure to have learnt the terms, like sin (sine), cos (cosine), tan (tangent) etc. Our ancestors had profound knowledge of trigonometry, which is clearly visible from the tables of values found out by them for the sin of different angles. The parallel terms used by them for sin and cos were respectively ज्या and कोज्या. Note that these terms are parallel and not the synonyms. This needs to be specified or emphasized, for, many a time, we tend to form and express our opinion, based on inadequate information! Whether you congratulate or condemn, when your opinion is based on incomplete information, you are committing a sin!
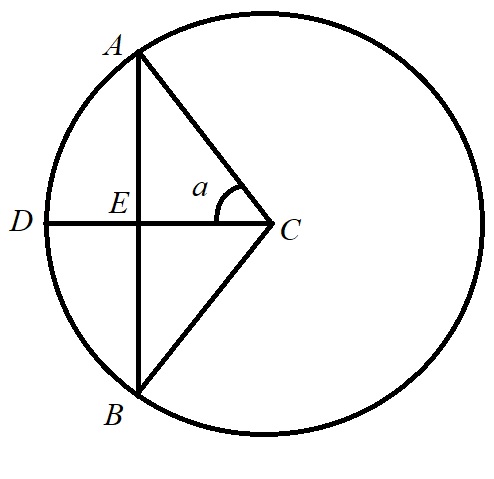
The values of ज्या for certain angles are 225, 449, 671 etc. Now if we assume that ज्या is just a synonym for sin, then a common reader would be misled to believe that according to Indian mathematicians, values of sin of certain angle are 225 or 449 etc. But how would the value of sin of any angle exceed 1? This might create a feeling of distrust towards our own ancestors. Therefore, it is said above that the terms ज्या and कोज्या are parallel to sin and cos, and not the synonyms. The exact meaning of these terms would be clear from the figure.
In the above figure, C is the centre of a circle, AB is a chord and CD is perpendicular to AB, intersecting AB at E. If the angle ACE is a, then ज्या a is AE, while कोज्या a is CE. Obviously, the values of ज्या and कोज्या for an angle cannot match with the modern values! So far, so good! But then what is the use of such values? Note that the radius of the circle is fixed, 3438. It is not just any circle! And now, if the values 225, 449 etc. are divided by 3438, we do get the values, which are very close to the modern values. For example, ज्या 30 is 1719. Divide it by 3438. We get 0.5, which perfectly matches with sin 30 degrees. Indians didn’t have any term (either parallel or synonym) for “tan”. The term उत्क्रमज्या stands for ED and should not be confused with “tan”.
Of course, to throw light on the reason of this discrepancy in the meanings of the terms, one will have to dig quite a bit. It’s not our concern, at present, so we will leave this topic here itself, but will certainly keep in mind the knowledge of trigonometry, that we had.
Since, we are dealing with similarity, let us delve a bit into music. In western culture, any note can be regarded as the base note (सा) and you get a typical octave (or सप्तक) with respect to that note. However our texts specify the frequencies of सा, रे, ग, and so on. In fact, for specifying the frequencies of various musical notes, many different sounds available in nature were referred. For example, Amarkosha specifies that the peacock’s sound was referred as सा, while the cuckoo’s sound was referred as प and so on. So Western music is liberal for the base note, while original Indian music seems to be particular with each musical note. It is for this reason that the instruments like, harmonium, piano, accordion are said to be unsuitable for Indian classical music. A musical melody C, E, G is “similar” to C#, F, G#. Such transformation from one scale to another seems perfectly okay in Western music, but perhaps in our culture and music it was not allowed. Don’t we find the same picture in maths? While in modern mathematics, any right angled triangle can be considered for trigonometry, our ancestors seem to be particular about the size of the triangle. One may say that western world is more liberal. One may say that we were more disciplined!
We mentioned the areas and volumes of geometrical shapes. If all the sides of a triangle are known, then can we find area of the same? The answer is affirmative. This is called the Heron’s formula, but it was known to Brahmagupta, another mathematical genius of India. A question naturally strikes, why not have a similar formula for obtaining area of a quadrilateral then? The reason is straight forward. With only four sides of a quadrilateral are given, the area of the same is not fixed. After this also, if one tries to seek the area of a quadrilateral with only side lengths given, then observe what Bhaskaracharya says on this…
स पृच्छको पिशाचो वा वक्ता वा नितरां तत:।
यो न वेत्ति चतुर्बाहुक्षेत्रस्यानियतां स्थितिम्॥
(sa pruchchhako pishaacho vaa vaktaa vaa nitaraam tata:|
yo na vetti chaturbaahukshetrasyaanitaraam sthitim||)
This roughly means the one who asks (or tries to answer) such a ridiculous question must be a (पिशाच) fiend!
The existence of the formula for the area of a triangle, only based on its sides, suggests that we were aware of the fact that with three sides given there exists one and only one triangle. This is, of course, just a guess, because two distinct triangles can have same areas. The non-existence of such a formula in case of quadrilaterals suggests that they knew that there are different quadrilaterals possible, with given sides.
Indians took keen interest not only in polygons but also in the circle. Attempts were made to obtain the circumference and area of a circle. The value 22/7 is known to us. We call it pi (π). However pi is not exactly equal to 22/7 and so a circle with diameter 7 units cannot have diameter of the length 22 units (exactly). It would be close to 22. This closeness was indicated by the word स्थूल. Bhaskaracharya says –
द्वाविंशतिघ्ने विहृतेऽथ शैलै:। स्थूलोऽथवास्याद्व्यवहारयोग्य:॥
(dvaavimshatighne vihruteऽtha shailai:| sthooloऽthavaa syaadvyavahaarayogya:|| )
If the diameter of a circle is multiplied by 22 and then (the product) is divided by 7, it gives approximate (or practically acceptable) value of the circumference of the circle.
The interest in the circle led Indians to think of spheres too. It’s really praiseworthy that they tried to obtain radius of celestial objects like the earth, moon etc. Not only they got very accurate figures, through this they also proved that earth was spherical in shape, well before other cultures did. If the Western world had studied Indian texts more seriously in those days and joined hands with Indians, the wonders of science and technology might have become known to the world much earlier than it did.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.