Introduction
In the famous book, ‘Arthashastra’ by Chanakya, various units of measurement used in ancient India have been mentioned. The base unit mentioned therein is ‘angula’. Although, the relationship of ‘angula’ with other units like ‘Dhanusha’ and ‘Yojana’ used in those days has been given, their relationship with the modern units such as centimetre and inch has obviously not been given, since these units were not available at that time. ‘Angula’ is considered to be the (average) width of a human finger, because ‘angula’ literally means finger. These days, this thickness is taken as 1.763cm. Several researchers have analysed the dimensions of ancient towns, buildings and other structures to find the value of ‘angula’ used in ancient India. A critical review of this methodology shows that the value of the standard ‘angula’ cannot be found this way. In this article, the value of ‘angula’ has been derived from the precise scale found during the 1930-31 season of excavation at Mohenjo-daro. This precise scale (dated 3500 BC or earlier) has equally spaced markings on a broken ‘shell’. From this scale, the value of ‘angula’ has been found to be precisely equal to 1.6764cm. On analysis of all seven ancient scales found so far – six in India and one in Sumeria (dated 2175 BC) – it is found that all the seven ancient scales are based on the precise value of ‘angula’ as 1.6764cm. It is further found that the standard street widths of the ancient towns, and also the standardised size of bricks are also based on this unit of ‘angula’, i.e. 1.6764cm. Interestingly, the name ‘Mile’ of the modern unit of distance is based on its relationship with the ancient Indian unit. Also, the speed of light given in the ancient Vedic literature, when converted into modern units, is found to be precisely equal to the speed of light in modern science, with zero error. It cannot just be a coincidence.
The Precise Scale
In his 1930-31 season at Mohenjo-daro, Ernest Mackay discovered a broken piece of shell bearing 8 divisions of 6.7056mm (0.264 inches) each, with a dot and circle five graduations apart[1]. It may be noted that the interval of the 5 divisions, works out to 33.528mm (1.32 inches). This measure is widely known as the Indus Inch.
Units of Length in Chanakya’s Arthashastra
Chanakya was the political mentor of the legendary Indian monarch Chandragupta Maurya. He was a man learned in many disciplines and wrote the famous book Arthashastra. In the Arthashastra, Chanakya mentions two types of Dhanushas as units for measuring lengths and distances. One is the ordinary Dhanusha, consisting of 96 Angulas, and the other Dhanusha is mentioned as Garhaspatya Dhanusha and consists of 108 Angulas, used for measurement of roads and distances. Chanakya also mentions that a Yojana consists of 8000 Dhanushas.
Decoding the Mohenjo-daro Scale
Taking an Indus Inch i.e. 5 divisions of the Mohenjo-daro scale to be equal to 2 Angula, the precise length of an Angula works out to be 16.764mm (0.66 inches).
A Dhanusha of 96 Angulas = 96 × 16.764mm = 1.609344m (1)
A Dhanusha of 108 Angulas = 108 × 16.764mm = 1.810512m (2)
A Yojana = 8000 Dhanushas(of 108 Angulas each) (3)
= 8000 × 1.810512m = 14.484096km (4)
Further,
14.484096km = 9 miles,(exactly!). (5)
Also, 1000 Dhanushas of 96 Angulas each = 1 mile (6)
Interestingly, when we look into the history of the unit mile, we find that the word mile is derived from mille, which means a thousand.
Other Ancient Scales
The Gudea’s Rule
The Gudea’s Rule (2175 B.C.) preserved in the Louvre shows intervals in Sumerian Shusi of 0.66 inches[2], which is exactly equal to the Indus-Saraswati ‘Angula’ of 16.764mm.
It may be observed that Prof Berriman of Oxford University, in his book[2] published in 1953, has clearly pointed out that “The principal unit of the linear scale engraved on a fragment of shell found at Mohenjo-daro in the Indus Valley measures 1-32 inches = 2 Sumerian shusi”, literally meaning finger or ‘angula’. Thus an ‘angula’ = 0.66 inch or 1.6764 cm. However, the later researchers have conveniently overlooked this fact, while determining the length of ‘angula’ in ancient India.
It is not a coincidence that the unit of Gudea’s Rule found in Sumeria, the earliest Mesopotamian civilization, was precisely equal to the Indus Angula. In a letter published in the weekly Illustrated London News, dated 27th September, 1924, A.H. Sayce, an Assyriologist, pointed out that the seals found in Mohan-jo-daro looked very much like ‘Proto-Elamite’ tablets found in Susa, the capital of Elam, an ancient culture related to the Mesopotamian civilization located in today’s Southwestern Iran, and the Proto-Elamite tablets were dated to the third millennium B.C. It proved that the citizens of Mohenjo-daro were in contact with the Sumerians[1]. That is why the standard units of measurement in the Indus Civilization and Sumerian Civilization were the same. In the Sumerian Civilization, it was named ‘Shusi’, which literally means finger. In the Indus-Sarasvati Civilization, it was named ‘Angula’, which also means finger.
Temple Wall-Engravings
Two engravings on a wall of the temple at Tiruputtkali (12th Century A.D.) near Kanchipuram, show two scales[3] one measuring 7.24 metres in length, with markings dividing the scale into 4 equal parts, and the second one measuring 5.69 metres in length and markings dividing the scale into 4 equal parts. It may be observed that each division of the first scale is precisely equal to a Dhanusha of 108 Angulas of 16.764mm each. Interestingly, the second scale is precisely equal to π times Dhanusha i.e. equal to the circumference of a circle with one Dhanusha as its Diameter.
The Lothal Ivory Scale
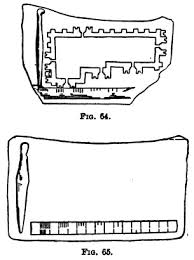
The total length of this scale is 4.6cm 46mm, There are a total number of 26 markings on this scale (figure 1), thus dividing the scale into 25 intervals. However, two of the intervals are much wider than the remaining 23 intervals. These two intervals are approximately of twice the width of the other intervals, clearly indicating that the two markings in these intervals have been erased due to weathering effect. Thus, the total number of intervals would be 27. Rao[4] as well as Mainkar[5] have correctly taken the number of divisions as 27 while working out the length of the smallest unit on this scale, and found the value to be 1.70mm, which is close to one-tenth of an angula of 1.6764cm. Taking each unit of this scale to be equal to one-tenth of an ‘Angula’ the total length of the scale works out to be 45.3mm. The difference of 0.7mm can be assumed to be an error in measurement.
The viewpoint of Michel Danino[1] that the number of divisions on the scale should be taken as 26 is totally wrong. Moreover, the number 27 makes the total length of the scale to be equal to 2.7 Angulas, which is precisely 1/40th of a Dhanusha of 108 Angulas.
Kalibangan Terra-cotta Scale
There are a total of 14 markings on this scale (figure 2) dividing the scale into 13 intervals. 7 of these intervals are precisely equal to each other, i.e. 4.6mm each. The other intervals are unequal, ranging from 3.3mm to 17.5mm. It may be observed that each of the 7 equal intervals is precisely equal to one tenth of the total length of the Lothal ivory scale, clearly indicating that the basic unit of these two scales is the same. Each equal division of the ‘Kalibangan’ scale works out to precisely 0.27 Angula of 1.6764cm or 1/400th of a Dhanush of 108 Angula. The other divisions on this scale are 3.3mm, 5.0mm, 6.7mm, 8.3mm, 11.0mm and 17.5mm. These are precisely equal to 0.2 Angula, 0.3 Angula, 0.4 Angula, 0.5 Angula, 0.67 Angula and 1.04 Angula respectively11. The total length of the scale adds up to precisely 5 Angula.
The different precise divisions of this scale indicate that this scale was meant for precise measurements up to an accuracy of 0.01 Angula. This is the most sophisticated scale out of all the ancient scales so far found.
The Harappa Bronze Scale
This “scale” is a broken piece of bronze rod of a little more than 3.2mm diameter, and only about 3.8cm in length. It has only four complete divisions which are marked off by V-shaped indentations. The values of the divisions are 0.960cm, 0.905cm, 0.945cm, and 0.925cm, averaging 0.934cm.
The V-shaped indentations and the small diameter cylindrical rod of bronze indicate that it is not a scale but a piece of metal rod meant to be bent into a ring making the rim of a circular wheel. It is improbable that anyone would use V-notches as markings of a regular scale. The original rod must have been long enough to make up the rim, but only a broken piece of the original rod has been located in the excavations. A little bit of calculation will indicate that it was probably a ‘Nakshatra Chakra’ (a wheel with 27 spokes, depicting the 27 stellar constellations) in making. The V-shaped notches were meant to fix the spokes into the peripheral rim of the wheel. The spacing of the notches indicates that the diameter of the wheel was precisely equal to 48 Angula of 1.6764cm each, i.e., half a Dhanush of 96 Angula. The spacing of the V-notches for a wheel of half-Dhanush diameter works out to 9.36mm which is very close to the average of the spacings marked on the rod.
It clearly shows that the basic unit used for this ‘Nakshatra Chakra’ was the same, i.e. 1.6764cm ‘Angula’.
Correlation with Dimensions of Ancient Structures
Mohenjo-daro’s Great Bath
The height of the corbelled drain forming the outlet of Mohenjo-daro’s Great Bath[6, pp. 133-142] is about 1.8m, which is equal to a Dhanusha of 108 Angulas of 16.764mm each.
Standard Street-Widths
Kalibangam, a city in the Indus-Saraswati Civilization (in Rajasthan, India) had street widths[7] of 1.8m, 3.6m, 5.4m and 7.2m i.e. built to the standard dimensions being equal to 1 Dhanusha, 2 Dhanushas, 3 Dhanushas and 4 Dhanushas respectively. Such widths are found at other sites also. Bigger streets of Banawali[7] another town in Indus-Saraswati Civilization (in Haryana, India) measure 5.4m i.e 3 Dhanushas.
Taj Mahal
A Persian manuscript “Shah Jahan Nama” contains a very particular description of three principal buildings of Agra – the Taj Mahal, Moti Masjid and Jamah Masjid. In the “Shah Jahan Nama”, the dimensions of these three buildings are given in Gaz. These dimensions were got measured by col. J.A. Hodgson in December, 1825, in feet and inches[8]. Barraud[9, pp. 108-109, 258-259] has taken a Gaz to be equal to 80.5cm which is precisely equal to half a Dhanusha of 96 Angulas.
It indicates that the unit of measurement used in Mughal period was related to the Indus-Saraswati unit.
Mayan City in Mexico (North America)
Drewitt[10] and Drucker[11] made a study of the ancient city of Teotihuacan, belonging to the Mayan Civilization , in Mexico, and hypothesised a unit of 80.5cm, which is precisely equal to half a Dhanusha of 96 Angulas, indicating that in ancient American continent, the units of measurement were the same as those in ancient India.
Critical Review of Value of Angula
R. Balasubramaniam has written two articles[12, 13] in which he has analysed the dimensions of Delhi’s Iron Pillar. In the first article, he assumed an Angula of 2.54cm, and, upon analysis of the dimensions of the pillar, he concluded that the ancient Angula was 2.54cm. In the second article, he assumed an Angula of 1.763cm, and, upon analysis of the dimensions of the pillar, he concluded that the ancient Angula was 1.763cm. He has further observed that “even if the Angula had been taken as 1.75cm or 1.77cm, the errors would have been similarly low”. He is perfectly right. However, his observation can be further extended and it can be proven that the error would be similarly low with any assumed value of Angula – be it 2.54cm, or 1.763cm, or 1.75cm, or 1.77cm or 1.6764cm or any other arbitrary value. Thus, with similar errors (called low by the author), one may assume any value of Angula and prove it to be correct. In fact with an angula of 1.6764cm, the percentage error works out to be much lower.
Most of the other authors have followed a similar procedure for analyzing the dimensions of various ancient structures to “prove” that the unit of length assumed by them was correct, with similar low errors.
Michel Danino in his article, Unravelling Dholavira’s Geometry[14], has gone a step further. He starts with the statement, “Dholavira’s engineers must have used a precise unit of length to measure or calculate the various dimensions involved. This unit can be calculated without any prior assumption”. He further says, “Let us name this unknown as D (for Dholavira)”. And, “The smallest dimension among those we have considered is the average thickness of the castle’s Western and Eastern fortifications, K.” By the way, he has conveniently ignored the fact that the smallest dimension is in actuality the castle’s Northern and Southern fortifications which is 13m, as against the 18.5m of the other sides. It is evident that some prior assumption was in his mind while selecting K = 18.5m instead of 13m which was clearly the smallest dimension. However, let us leave this intentional overlook and move further.
After deriving several equations based on the assumed proportions of the various dimensions, and again, ignoring one of the “inconvenient” proportions, he has arrived at the conclusion that K = 10D.
Now with K = 18.5, D worked out to be equal to 1.85m, which he rounded off to 1.9m (again, clearly with some prior assumption in mind). If he had to round it off at all, then why not to 1.8m which is equally far from 1.85m, or to 1.81m, which is closer to 1.85m than 1.9m is to 1.85m? His claim of “no prior assumption” is deceptive. It may be observed that with D=1.81m the percentage error in various dimensions works out to be much lower than with D = 1.90m.
Further steps for “proving” that the errors with this unit are as low” are similar to those of the analysis of the Delhi Iron Pillar dimensions by R. Balasubramaniam. The percentage error for various dimensions goes upto 3%. For determining the value of a standard unit, to call such error percentage as low is entirely unscientific.
Michel Danino[1, pp 106] has mentioned that 7 x 14 x 28cm bricks were most commonly used for houses, and 10 x 20 x 40cm or a little more for the city walls. In fact, Kenoyer[15] has mentioned that the bricks used for houses varied in size from 6.5 x 13 x 26cm to 7 x 15 x 29cm. These were obviously not standardised sizes. The standard size might have been in between these dimensions. However, the bricks used in city walls were probably standardised. The size 10 x 20 x 40 or a little more clearly depicts that the standardized bricks measured 6 x 12 x 24 Angula of 1.6764cm, giving a size of 10.06 x 20.12 x 40.24cm, which is a little more than 10 x 20 x 40cm.
The Angula of 1.763cm must be discarded as there is no scientific proof to show that this Angula was used in the Indus-Sarasvati Civilisation. It should be replaced by an Angula of 1.6764cm, which precisely fits in with zero error into all the ancient scales found so far, viz.
1. The Mohan-jo-daro Scale
2. The Sumerian Gudea’s Rule
3. The Lothal Ivory Scale
4. The Kalibangana Terra-cotta Scale
5. The Bronze “Scale” of Harappa
6. The two scales engraved on the walls of the ancient temple at Tiruputkali near Kanchipuram in South India
Considering that this unit is also related to the modern ‘mile’ with absolutely zero error, not an iota of doubt is left that the Angula of 1.6764cm was the standard Angula of Indus-Sarasvati Civilization.
Speed of light in Vedic Literature
In the commentary on Rig-Veda, Mandal 1, Sukta 50, Mantra 4, Sayanacharya (14th Century AD) writes:
तथा च स्मर्यते…
योजनानां सहस्रे द्वे द्वे शते द्वे च योजने।
एकेन निमिषार्धेन क्रममाण नमोस्तु ते॥
“Salutations to Thee (the Sun) who approacheth (at a speed of) 2202 yojanas in a nimishardha.”
Clearly it is the Speed of light(or sun-rays) that is mentioned in the shloka. This shloka is attributed[16, pp. 67] to the son of Kanva Maharshi (5th millenium B.C.).
To put it in mathematical terms, as stated by the above shloka, the speed of light would be:
Speed Of Light = 2202 Y ojanas/Nimishardha (7)
As we have calculated earlier, a Yojana = 14.484096 Km. For the value of Nimishardha, we refer to Vishnu Purana (Book 1, Chapter 3, shloka 8,9), wherein it is stated that:
15 Nimishas = 1 Kashtha 30 Kashtas = 1 Kala 30 Kalas = 1 Muhurta 30 Muhurtas = 1 day & night (अहोरात्रम्)
Thus,
one day & night = 405,000 Nimishas = 810,000 Nimishardhas. (8)
(Literal meaning of Nimishardha being half a Nimisha).
In Surya Sidhanta (Chapter 1, Shloka 12), it is stated that 60 Nadis constitute one Stellar Day and Night (नाक्षत्रम् अहोरात्रम्). It is also well known that a Muhurta = 2 Nadis. It is clear from this that in Astronomical calculations, the stellar day was taken as the unit of time. A stellar day is the time taken by the Earth to complete a rotation around its axis (with respect to stellar constellations). A stellar day is equal to 23 hours, 56 minutes and 4.1 seconds, or equivalently 86,164.1 sec, as the stellar constellation make 366.25 relative revolutions in a year of 365.25 days.
So,
Nimishardha = 86164.1/810000 sec = 0.1063754sec (9)
The speed of light as given in the Vedic Literature therefor comes out to be:
2202 * 14.484096 / 0.106375 km/sec = 2.998 × 105km/sec (10)
which is precisely equal to the speed of light as per the latest modern measurements.
Conclusions
- From the above, the following conclusions can be drawn:
The basic unit of length measurement in the Indus-Saraswati Civilization was an Angul of 16.764mm. This unit was used not only in the Indus-Saraswati Civilization, but also in South India, and other ancient world Civilizations including Sumerian and Mayan Civilizations. - The modern age concept of globalization was an established way of life in the Vedic/Indus-Saraswati Civilization era, as proven by the shared unit of length measurement found across far-flung cultures spread over Asia, Europe and America.
- The Speed of Light as given in the Vedic literature, is precisely equal to the Speed of Light as per modern measurements, which shows that during the period 5000 B.C. to 3000 B.C., Science and Technology was very much advanced, which was somehow lost during the medieval ages.
References
[1] Danino, Michel The Lost River – On the Trail of Saraswati, Penguin
Books, 2010.
[2] Berriman, A. E. Historical metrology, a new analysis of the archaeological and the historical evidence relating to weights and measures., Dent, 1953.
[3] James Heitzman and S. Rajagopal, Urban Geography and Land Measurement in the Twelfth Century : The Case of Kanchipuram, The Indian Economic and Social History Review. SAGE, 2004
[4] Rao, S.R. Lothal, a Harrapan Port Town (1955-62). New Delhi: Archeological Survey of India, 2 vols., 1979
[5] Mainkar, V.B. Metrology in the Indus Civilization, in Frontiers of the Indus Civilization, eds. B.B. Lal & S.P. Gupta. New Delhi: Books and Books, p141-151., 1984
[6] Jansen, Michael Mohenjo-daro: architecture et urbanisme, Les cités oubliées de lÍndus: Archéologie du Pakistan, 1988.
[7] Lal, B.B. The Earliest Civilization of South Asia, Aryan Books International, New Delhi, 1997
[8] Hodgson, Col. J.A. Memoir on the Length of the Illahi, Guz, Journal of
the Royal Asiatic Society of Great Britain and Ireland., 1840.
[9] Barraud, R.A. The Complete Taj Mahal and the Riverfront Gardens of
Agra (ed. Koch E.) Thames and Hudson. London, 2006.
[10] Drewitt Measurement Units and Building Areas at Teotihuacan, 1987
[11] Drucker, R. David. Precolumbian Mesoamerican Measurement Systems: Unit Standards for Length, 1977
[12] Balasubramaniam, R. New Insights on the Corrosion of the Delhi Iron Pillar Based on Historical and Dimensional Analysis, Current Science, Vol. 73, No. 12, 1997
[13] Balasubramaniam, R. On the Mathematical Significance of the Dimensions of the Delhi Iron Pillar, Current Science. , 2008
[14] Danino, Michael Unravelling Dholavira’s Geometry. In P. Chenna Reddy (ed.), Rama Vijayam: Recent Researches in Archeology, History and Culture (Fetschrift to Prof.K.V. Raman). Delhi: Aam Kala Prakashan, p179-93., 2010
[15] Kenoyer, Jonathon Mark. Ancient Cities of the Indus Valley Civilization. Karachi & Islamabad: Oxford University Press & American Institute of Pakistan Studies., 1998
[16] Pride of India, Published by Sanskrit Bharati, 2006.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.