Towards the end of the 12th century, the Islamist raider Bakthiyar Khilji ransacked the ancient Buddhist university of Nalanda in eastern India. Apart from the many students and monks who lived there, the monastery also housed a large library, similar in extent to the great library of Alexandria in Egypt. After he looted the wealth of the monastery and put to death many monks, Bankthiyar Khilji was asked to decide on what to do with the books in the library.
Khilji first asked if there was a copy of the Quran in the library. The answer was negative. He then asked to burn all the books in the library. “But valuable knowledge in the books will be lost forever”, warned the caretakers of the library. Khilji famously answered as follows
“If there is a book that says anything against the teachings of the Quran, then it is blasphemous and should be burned. If there is a book that agrees with the teachings of the Quran, then it is superfluous and should also be burned. Please take care that no book is left unburned.”
The Persian historian Minhaj-i-Siraj who was accompanying the raid recounted that the fires from the embers of the library kept blazing for several days. This action might horrify us today on account of its senselessness and violence, but there is a twisted logic to what Khilji said in defense of burning the books. An echo of this logic can be found in the pronouncement of George W. Bush after the 9-11 attacks on New York City in 2001.
“You are either with us or you are against us!”
Bush did not see any shades of gray in the vast canvas of the political landscape of the world. Similarly, Khilji classified knowledge in a strict binary fashion: that which is in agreement with the Quran and that which is not in agreement. He considered Quran itself as all-encompassing in knowledge, so this strict binary classification precipitated his decision.
But what was lost in the many books burnt in Nalanda was not only a vast compendium of facts and knowledge but also a philosophical commentary on the limitations of binary classification of knowledge.
Indeed, the most profound examination of these limitations was done by Nagarjuna, a Buddhist scholar, who many centuries earlier had served as a rector to the Nalanda University, in the third century AD. But what Nagarjuna elaborated on was an even more ancient tradition from India, tracing its roots at least three thousand years deeper into history when it was codified in the Vedas – the holy scriptures of the Hindu religion.
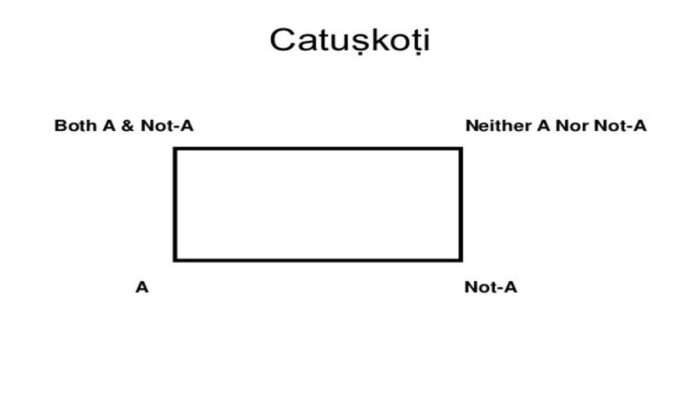
According to our tradition, logic is not 2-valued (as commonly understood as true/false), not even 3-valued (as commonly understood to denote shades of gray), but is 4-valued.
This 4-valued logic is known in Sanskrit as Chatuskoti. For a long period of human history, this logic reigned supreme in Asia. Eminent philosophers and logicians in China, Japan, and Southeast Asia have painstakingly translated the Buddhist scriptures into their native languages, the most cherished ones being the commentaries written by Nagarjuna.
Negation is the most elementary operation in language. We cannot think without using negation on different concepts and ideas. But every time we apply negation, we are introducing a strong bias into our thinking, which will eventually lead us to severe errors and paradoxes. Considering 4 sides to a negation, instead of the usual 2 sides, can bring greater clarity in this regard.
Chatuskoti or the 4-sided negation
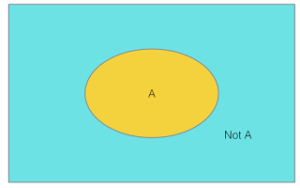
Figure 1: Venn diagram illustrating binary logic
Let’s consider a simple proposition “Cheetah is the fastest animal” and denote this by the symbol A. In regular logic, this proposition is either true or false. When we think of a proposition, we usually visualize it in the mind’s eye on a straight line-segment: akin to a barometer of falsehood. On one end lies truth and on the other end lies falsehood.
When we are certain of the truth value of a proposition, this line-segment dissolves into two tiny dots, standing apart from each other, which we can call “A” and “Not A”. However, this visualization is incorrect.
Instead, what we need to visualize is the Venn diagram shown in Fig 1. When we frame a proposition, we create an island “A” in a vast sea of possibilities, known as the universe Ω. When we use strict binary logic, we associate “Not A” to everything in this Ω except the island denoted by A. Depending on how many words we use to describe A and how clearly we describe it, our knowledge of this island increases.
But the vast sea surrounding this island can be still a mystery to us. For example, to elaborate on our example, a Cheetah can be described as a wild cat with a yellow fur coat and spots, that it is native to Africa and that it hunts gazelles. To go to the extreme, we may describe it by giving the entire genome of Cheetah in the code of DNA. But what exactly is “Not A”, what differences to the genome of Cheetah will classify it as a Non-Cheetah?
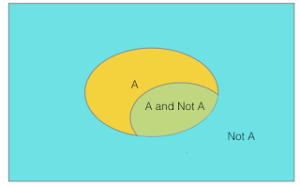
Figure 2: Venn diagram illustrating fuzzy or probabilistic logic
As our knowledge about other animals increases, we can measure our understanding by creating an island of ambiguity “A and Not A” that is encroaching into the island of “A” in the Venn diagram. This island measures the ambiguity of the proposition, inherent to the finite length of the description of A.
As we conduct experiments into how fast Cheetahs run as opposed to other animals, we can measure the probability of A being true. Ideally, this island of ambiguity shrinks and we get back to our binary world.
But in reality, we still have no complete knowledge of the universe Ω. What exactly is an animal? How many other animals do we know? What exactly do we mean by “fast”? Can bacteria floating in rapid ocean currents be considered animals? This is a case we have not considered when we framed proposition A.
Unlike the island of ambiguity, this uncertainty is not related to A, but to the universe Ω. It specifically refers to the limitations of our understanding when we say “Not A”, its overlap with Ω is not as complete as we imagine it to be. If we correct for this, we obtain a visualization of the 4-valued negation as follows.
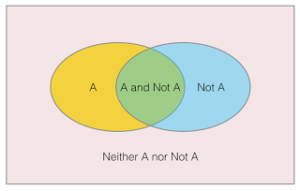
Figure 3: Venn diagram illustrating Chatuskoti, or the 4-sided negation.
This 4-sided negation creates four distinct zones in the universe Ω. With increasing knowledge, our understanding of all these 4 zones increases, but the zone of “Neither A nor Not A” may remain forever. This is because we may predict that we don’t know something about the universe, but we may not be able to express exactly what it is that we don’t know.
Please note that this limitation is due to two things: (1) our understanding of the world and (2) the limited expressibility of language. Even if we allow humans to be omniscient (in whatever finite context for Ω specified by our problem), the ambiguity in the language may never be resolved.
Indian logic is rather unique in modeling this bias due to language. For instance, in Ganita (Indian mathematics), proof by contradiction is rarely used. And only for proving non-existence, not for the existence of an object. In the Nyaya syllogism, an example (Drstantha, literally “end of sight”) is provided before a generalization is applied to a related object.
Jain logic uses a similar tool known as “syad-vada” explicitly marking the hypothesis at each step and not making premature generalizations. The Indian tradition of debate, known as “Samvada”, requires an elaborate method of re-stating the argument of the opponent in a satisfactory manner, termed as “Purva Paksha”.
It is understood that many philosophical perspectives (Darshana, literally “view”) can all have valid claims to truth, though they conflict with each other by word. Such respect to multiple claims to truth, or caution against blunt categorization of concepts, is not present in Western logic.
How did the European renaissance miss the 4-sided negation
In the 18th century, when the European renaissance was in full steam, Immanuel Kant said that Aristotle discovered everything there was to know about in logic. A bit later, Hegel agreed to say that logic has not evolved since Aristotle’s times.
Such arrogance from European thinkers is puzzling, because they definitely came into contact with Indian science and mathematics, but apparently not Indian logic. Aristotle’s logic uses the 2-sided negation and forms a trivial subset of the Indian Chatuskoti, where the bias from the language is ignored. There exists a funny anecdote where this limitation is demonstrated to Aristotle by the cynical philosopher Diogenes.
Apparently, Aristotle defined man as a “featherless two-legged animal”. Diogenes picked a chicken and plucked its feathers and presented it to Aristotle, saying “There is your ‘Man’ “. This mockery got Aristotle to give a new definition of man as a “featherless two-legged animal without webbed feet.” Unfortunately, Aristotle completely missed the point of Diogenes, which was that language was inherently biased.
This foolish and blind trust in language led Europeans to champion the “axiomatic method” for mathematics, attributed to Euclid. For many centuries, Europeans celebrated a trivial derivation of the Pythagoras theorem by Euclid as the ultimate demonstration of the axiomatic method, without making use of any perceptive validation.
Comically, this proved to be wrong as the haloed Euclidean method indeed used a visual check in one of its proofs. This was corrected only by Russel and Whitehead in the 20th century, bloating the length of the axiomatic derivation of this trivial result, all the way blindly following 2-sided logic. As we investigate how and why the European renaissance missed the 4-sided logic, we have to inspect the life of one of its pioneers – Ramon Llull.
Ramon Llull was a Catalan philosopher in the 13th century who was critically important for the historical development of the European renaissance. He had traveled extensively and spent a significant amount of time in North Africa, conversing with Arabs in the Moorish centers of learning. During his time (roughly termed the Middle Ages), Europe had sunk into the depths of ignorance, with the classical discoveries of Greece and Rome forgotten.
In contrast, Arab civilization was in full flourish, where the Arab mathematicians and astronomers had compiled and built upon the knowledge from multiple lands ranging from Greece to India and China. It was the contact with Arabs, in southern Spain and Italy that sparked the fire of European scholarship. Ramon Llull was a critical piece of this puzzle.
Arab astronomers were interested not only in mapping the course of the stars and the planets but also in understanding how this connects to human psychology. These esoteric sciences of astrology, alchemy, and parapsychology are shunned today as superstitions, but in earlier periods, all scientific investigation was done at the behest of such esoteric subjects.
The fundamental goal of these scientists was to liberate the human condition from suffering and achieve harmony with the universe, the objective study of natural phenomena was only a means to this end. The harbinger of modern science, Issac Newton, was himself a practitioner of alchemy. With Ramon Llull, these lines were blurred even further. The Arab astrologers were developing upon the ancient science of Indian astronomy and astrology (known as jyothisha).
In ancient Indian mythology, the circle denoted the universe and the square denoted the human understanding of this universe. The Vedic sacrifice required a mathematical understanding of how to convert a circle into a square. These esoteric ideas spurred a lot of mathematical development – arithmetic, algebra, trigonometric functions, infinite series, and so on.
Many of these ideas reached Europe via an Arab translation of an Indian text called Brahmaguptasiddhanta, (translated into Arabic as Zij-al-Sindhind by the astronomer Muhammad al-Fazari). The Arab astrologers codified these ideas into a mechanical system that makes the right predictions irrespective of who is using the system. In one form, this mechanical system became a device known as a Zairja – the first human imagination of an automaton.
Ramon Llull was deeply inspired by the Zairja and created an esoteric art of symbolism that he termed Ars Magna. This was supposed to represent all the aspects of the universe, as well as all the aspects of God. By representing all the possible aspects of knowledge in a cartographic manner, he created the first representation of “well-rounded” knowledge. He wanted to develop a mathematical automaton for debating with the Muslims, in order to win them over and convert them to Christianity.
The legend goes that he was pelted with stones in Tunis when he announced that his Ars Magna could not be understood unless the person accepted Christ as the savior. After his death, Llull was beatified by the church, but his most sincere disciple was burnt at stake. This was Giardano Bruno, who developed upon Ars Magna to denote all the cosmological concepts and who had come to the conclusion that sun was at the centre of the universe (and not the earth, as mentioned in the bible).
Galileo escaped a similar fate from the church by recanting his sayings, although he could see the motion of the planets in his telescopes. This uneasy relationship with astronomical, astrological, and esoteric sciences persisted in all Abrahamic faiths, with practitioners often being accused of worshipping the devil. This is inevitable because these sciences stemmed from pagan cultures like Greece and India.
The influence of Llull extended beyond astronomy. Leibnitz made his dissertation about Llull’s art, and this greatly influenced his future pursuits: calculus and logicism in philosophy. He called this Ars Combinatoria. Along with Newton, Leibnitz was the fundamental mover of the European renaissance in mathematics and physics.
Many mathematicians tried to follow in Leibnitz’s footsteps, to ultimately realize a consistent and mechanical system that can predict everything. The latest expression of this dream was by Hilbert, who tried to reduce all mathematics to a set of axioms. However, this adventure was cut short by Godel, who proved that inconsistencies inevitably will creep up in any system of axioms if it tries to be complete (describe everything).
This crazy pursuit in history has been described aptly by the computer scientist Gregory Chaitin (who along with Vladimir Kolmogorov is reckoned as the founder of the field of algorithmic information theory). To this day, the field of knowledge representation in computer systems, ranging from databases to the internet, is indebted to Ramon Llull and the Zairja of Arab astrologers.
The astonishing thing is that this historical line of development has completely missed the Catuskoti or the 4-sided negation in logic. It is a mystery why this has not reached Arab scholarship from India, and from there to Europe. It is unlikely that all the knowledge disappeared with the burning of the Nalanda library.
The only plausible explanation for why Arab and European thinkers ignored Indian logic was that it was extremely inconvenient to the organizing principles of their religions. After all, one cannot have “blind faith in the book of the lord” if one doubts the very nature of language.
If Llull was applying the Indian tradition of logic, he wouldn’t have expressed that the people of Tunis needed to convert to Christianity to understand his Ars Magna. He would know that Ars Magna will forever be a work in progress and forever be deficient of its goals. This was ultimately expressed in the late 1800s by Emil-du-Bois Raymond as “Ignoramus et ignoramibus”, and at that time, he was soundly ridiculed for saying this.
The history of western logic had another brief brush and fascination with India. The English mathematician George Boole was deeply inspired by Indian philosophy. His wife Mary Everest Boole, a significant mathematician on her own right, was the bridge to India. Her uncle Everest was a great adventurer in India and gave the eponymous mountain its name.
Mary Boole also was in correspondence with Jagadish Chandra Bose, who was a noted Indian scientist at that time. She wanted him to study the efforts of her husband, but this letter was left unanswered by Bose. George Boole developed an elaborate system of logical inference by using the principles of algebra, which he wanted to apply for esoteric ends (salvation, transcendence, etc.)
Nobody at that time believed that this system would have any practical use. This changed dramatically when Claude Shannon used Boolean logic as the basis for his mathematical theory of information. It is an open question if the development of information theory would have taken a different course if Boole incorporated the 4-sided negation into his logic.
However, this did not happen and computer systems today are mostly restricted to 2-sided or 3-sided logic. This opens the tantalizing possibility that a new and more general “mathematical theory of communication” is still waiting to be discovered by us.
This article was first published on India Facts.
Disclaimer: The facts and opinions expressed in this article are the personal opinions of the author. Indic Today does not assume any responsibility or liability for the accuracy, completeness, suitability, or validity of any information in this article.
Disclaimer: The opinions expressed in this article belong to the author. Indic Today is neither responsible nor liable for the accuracy, completeness, suitability, or validity of any information in the article.